Blog 4

Hello Class:

Today I am going to teach you about completing the square.

What does it mean to complete the square you ask?

Well! Let me tell you!

Completing the Square is used when solving general quadratic equations.

                                                                                 2       2
In Algebra a quadratic equation looks like this: ax   + by   + c


To solve a quadratic equation by completing the square.

All it takes are 




Be sure to follow along!



Step 1: Divide all terms by a (the coefficient of x2).
                        

Step 2:  Move the number term (c/a) to the right side of the equation.

Step 3: Complete the square on the right side of the equation and glance this                                                                     by adding the same value to the right side of the equation.


Step 4: Take the square root of both side of the equation.


Step 5: Subtract the number that remains on the left side of the equation to find x.



Example: x2 + 8x + 2


Step 1:    can be skipped because the coefficient of x2 is 1

Step 2:    x2 + 8x = -2

Step 3:    x2 + 8x + 16 = - 3 + 16  -> x2 + 8x + 16 = 13

                         2
               (x + 4)  = 14

Step 4: (x + 4) = 3.74
                  -4
Step 5:  x= .26

And thats the answer! That is how you solve for a quadratic equation by solving for the square.

Blog Post 3.5

I chose four websites that had games for kids about 12 years and older and that had large amounts of different games.

1.  http://www.math-play.com

A website designed to better your math skills wherever you have access to a computer.  The site has tons of different games to help you with math. The website has games split into different sections. Each category is either a level in math or a topic of math. An example would be 5th grade math or Integer games. This site is made for anyone between the ages of 7 and 20 depending on what math class you are taking.  The site has games that are appropriate up to college level calculus.  I would recommend this site to anyone looking to get some more on math and can't sit down at a computer.  The website has all sorts of games for any kind of learner or player.  The website has a good feel to it and is very organized.  If you are trying to learn more about math I definitely recommend this class. 

2. http://www.learningwave.com/abmath/

Learningwave.com holds a math game called Asburd Math.

Absurd Math is a mathematical solving questions type of game.  The player proceeds on missions in a fantasy world .  There are four different levels of the same game on the website.  This is too increase the difficulty for players as they beat some of the earlier levels.  This sight focuses on Pre-Calculus, but the four different levels include a lot more math then just Pre-Calculus.  I would not recommend this site because it does not have a lot of variety. If you get bored of the one game then there are no other games to play and all of a sudden the site is worthless.  The site needs to have more variety and then it will be a great site.

http://www.mathplayground.com/games.html

Mathplayground.com is a huge conglomerate of math games that are helpful no matter what you want to study.  The website is organized very well, which makes it easier to find what you want to do on the site.  There are games that are adding fractions while driving and other games where it asks you to fill in puzzles in order to move to the next level.  I firmly recommend this site as it is one of the far better ones out on the internet.  It has a lot of options to choose from and covers a large range of material so you will always have a new game to try if you run out of study options.

http://hotmath.com/games.html

While hotmath.com only has four games each game is intended for a separate audience.  There is Catch the Fly for middle school and up; Number Cop for middle school and up; Factortris for 9th and up; and Algebra vs the Cockroaches high school and up. The site is well organized and clean. I would recommend this site just based on the fact that all four games are fun. It also helps a lot with learning consequences in math

Blog 4- Elasticity

Caitlyn McMunn - The Chain Rule

The Chain Rule

Today, we will be talking about the chain rule.

How to explain the chain rule:

The chain rule is one formula that can be used to find the derivative of two functions. It can be used to find the derivative of more than two functions, but for the purpose of this lesson, we will only focus on two.

The chain rule states the following:

In this situation, A and B are functions.

(A(B))' = (A(B)) * B'

Recall Leibniz Notation: 

In Leibniz notation, this rule would be expressed as dz/dx = (dz/dy)(dy/dx)

Walking through an example:

Now that the chain rule has been explained, let's do an example!

First, note that the derivative of these two functions is d'(x)

Let's make f(x) = 4x + 3 and  b(x) = 2x + 4

First, we have to solve each one separately. So:

f'(x) = 4

and

b'(x) = 2

If we are using the chain rule, then d'(x) = f'(b(x)) * b'(x)

So

d'(x) = f' (2x+ 4) (2)

And then we simplify even more to

(4)(2) = 8

Now, let's try two examples on your own

1) f(x) = 5x + 1 and g(x) = -3x + 4

2) f(x) = 7x + 8 and g(x) = 6x + 5

Answers:

1) d'(x) = -15

2) d'(x) = 42 

finding distance

Good afternoon class, today we will be learning about how to measure distance traveled using left hand and right hand sums.

measuring distance when traveling at a constant velocity is relatively simple, just use the equation

Distance=Velocity x Time

For example, if Christine drove at 65 mph for 4 hrs., how far did she drive?
Distance= 65 mph x 4 hrs.
Distance =260 miles

It becomes slightly more difficult to measure distance when not travelling at a constant velocity, but it is simply a matter of a few extra steps.

For example, if Christine drove 80 mph for a 1/2 hr, 60 mph for 2 hrs, and 75 mph for an 3/2 hrs., how far did she drive?

Distance= (VxT) + (VxT) + ...

Distance = (80 x 1/2)+ (60 x 2) + (75 x 3/2)

Distance= 352.5 miles

another way to calculate distance would be to find the average of the left hand sum and the right hand sum.

T	0	2	4	6	8	10
MPH	60	62	65	68	69	70

 For example to calculate the left hand sum of the table above, you would find the distance the same way, but leave out the last two seconds.(T=10, mph= 70)

LHS= (60x2)+(62x2)+(65x2)+(68x2)+(69x2)

LHS= 648 miles

To calculate the right hand sum of the table above, you would use the same process as above, but instead of cutting out the last two seconds, you would cut out the first two.

RHS= (62x2)+(65x2)+(68x2)+(69x2)+(70x2)

RHS= 668 miles

calculating the average of the LHS and the RHS will give you a close estimate of the distance traveled. 

Average= (648+668)/2

Average=658 miles

That is how you find distance traveled using right hand and left hand sums, and tomorrow we will learn how to graph them. 

brian post 4

     Brian Hanus
     Local and Global, Maximums and Minimums

   Hello class, in today's lesson we are going to be covering how to find local and global maximums and minimums.

Being able to find these values is important because it allows you to find where a function is at its greatest or its smallest.  It also allows you to find a value within the function where it changes from decreasing to increasing or from increasing to decreasing.

First lets talk about what these terms mean:
Local:  The local maximum or minimum of a function is a point where there is a point with the largest or smallest value relative to the points around it.  There can be many local maximums and many local minimums.
Global:  The global maximum or minimum means that it is the value of a function that is the absolute largest or smallest.  There are no other values that are higher if it is the maximum or lower if it is the minimum.  There can only be one global maximum and one global minimum.
Maximum:  A maximum or "max" is a value that is the largest or larger compared to other values.
Minimum:  A minimum or "min" is a value that is the smallest or smaller compared to other values.

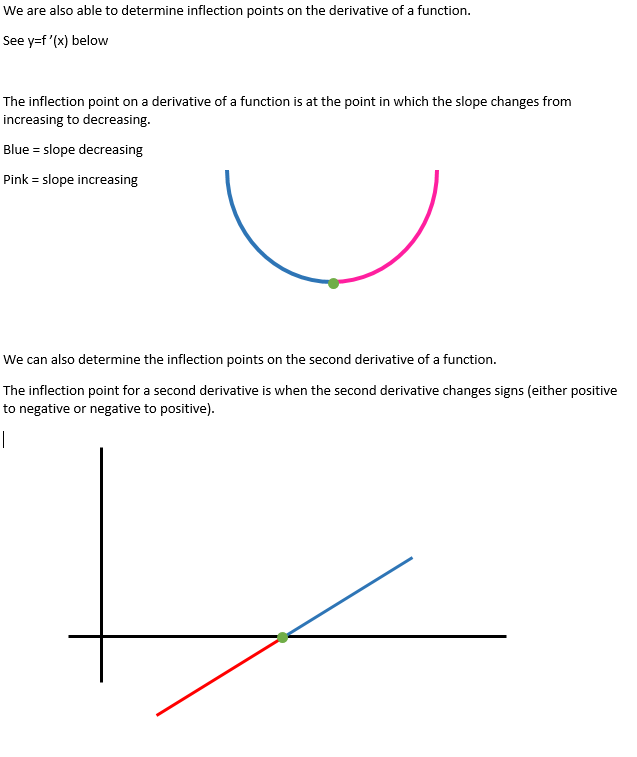
All of these concepts can be seen in this graph.


Now lets talk about how to find these values.  When you are given a function that you want to find these values, you can use the First Derivative Test.
The First Derivative Test is a process where you find the derivative of a given function and then set the derivative equal to 0.  When the derivative is equal to zero it means that there is a critical point.  A critical point can be a local or global, maximum or minimum.
It is a max when the derivative goes from positive to negative.
It is a min when the derivative goes from negative to positive.
It is not a max or min when it stays at negative when it was already negative or stays at positive when it is already positive.
A global max or min is either at the endpoints or a critical point.
Example of First Derivative Test:

On the interval [-2,3]
f(x) =  3x4−4x3−12x2+3


f'(x) =   12x3−12x2−24x
      =   12x(x2−x−2)
        =   12x(x+1)(x−2)
     0 =   12x(x+1)(x−2)
     x =    -1,0,2

Before -1 the derivative is negative:
12(-2)(-2+1)(-2-2)= -96
After -1 the derivative is positive:
12(-.5)(-.5+1)(-.5-2)= 7.5
This means that at -1 there is a min.
When plugged into the original function -1, gives an output of -2.
This means it is a local min.

Before 0 the derivative is positive:
12(-.5)(-.5+1)(-.5-2)= 7.5
After 0 the derivative is negative:
12(.5)(.5+1)(.5-2)= -13.5
This means that at 0 there is a max.
When plugged into the original function 0, gives an output of 3.
This means it is a local max.

Before 2 the derivative is negative:
12(.5)(.5+1)(.5-2)= -13.5
After 2 the derivative is positive:
12(3)(3+1)(3-2)= 144
This means that at 2 there is a min.
When plugged into the original function 2, gives an output of -29.
This means it is the global min.

At 3 the function gives an output of 30.  On the interval this is the global max.
So, x=3 is the global max, x=-1 is a local min, x=0 is a local max, and x=2 is the global min.

That is the end of today's lesson.  You now know how to find the local and global, maximum and minimum and what they mean.

Inflection Points

Mohamed Salahuddin Blog Post 4

Definite integrals and the area under a curve

In this topic I want to explain the Definite integrals, and explain its relation with the area under a curve.

A Definite Integral has start and end values: in other words there is an interval from “a” to “b”.

We can find the Definite Integral by first calculating the Indefinite Integral at points x, or I(x);

The second step is to find substitute the “a” and “b”, to find I(a) and I(b);

The third step is to subtract the I(a) from I(b) to obtain the Definite integrals.

Now, that we know how to solve it, we need to explain what does it mean. Say if it is a Definite integrals of the f(x) from “a” to “b”, it is represented by the area of the curve from the x-axis to the f(x) graphically.

If however f(x) is crossing the x-axis between the interval [a, b], we need to find the crossing point c, and integrated it in two parts, from [a, c] and [c, b].

Now we will use an example to illustrate my point.

Say if we want to integrate f(x) =x-2 from [2, 3].

Graphically, it is exactly the area between the f(x) =x-2 and x-axis from x=2 to x=3.

Now if we want to find the area between [1, 3], we need to be careful, since f(x) is crossing the x-axis within the interval at x=2. So we need to integrate two parts: [1, 2], and [2, 3]

The total area is thus 1+3=4.

Now we can see the close relation between the Definite Integral and areas under a curve. It can also be used to find volumes, central points and many useful things.

Limits - Muneera Albahar

My name is Professor Muneera Albahar and today I am going to teach you the concept of limits.

Learning Objectives:

1.     Understand the meaning of limits and why we study it.

2.     Learn how to calculate the limits for a specified function. (Students should be able to explain how they to come to a particular solution.)

3.     Real World Application

Learning Materials:

Youtube Video Link: http://www.youtube.com/watch?v=skM37PcZmWE

Reference Book: “Fundamentals of University Mathematics” by C M McGregor, John Nimmo, Wilson Stothers.

Website: http://www.sparknotes.com/math/calcab/functionslimitscontinuity/section2.rhtml

       http://www.mathsisfun.com/calculus/limits.html

Lesson Outline

Ø  Why we need to learn limits?

Limits are the most fundamental concept in Higher Mathematics, especially Mathematical Analysis. Most concepts, such as continuity, differential, integration, are defined on the basis of limits. For example, the definition of function continuity at a certain point is always written as the following:

“In the function f, at the certain point x₀ of its domain, if the limits of f(x) from left hand side and right hand side as x₀ approaches f(x₀) through the domain of f exist and both are equal to f(c)”.

To simplify, a limit is our best prediction of a point that we are unable to observe, which means that we can learn a lot about the function using limits. For example, we can check what happens to the function at a discontinuity by taking a limit at this point. Graphically, it also tells us that the function approaches either positive or negative infinity.  

Ø  Definition

In the 19^th century, Augustin-Louis Cauchy, followed by Karl Weierstrass, formalized the definition of the limit, which became widely known as the (ε, δ)-definition of limit.

Suppose f is a real-valued function, and c is a certain number of its domain. The expression  means when the values of x whose distance from c is less than some positive number δ, that is, values of x within either (c − δ, c) or (c, c + δ), there is a certain positive number ε which represent any small positive number, that f(x) certainly lies in the interval (L-ε, L+ε).

Ø  Graph Explanation

Whenever a point x is within in δ units of c, f(x) is within ε units of L.

Ø  Rules For Computing Limits

Three fundamental Rules:

1.     The limit of a constant will simply be the constant

2.     If two sequences have limits that exist, then the limit of the product is the product of the limits.

3.     If two sequences have limits that exist, then the limit of the sum of sequences is the sum of the limits of the sequences.

If our sequence is described by a fraction with powers of n on the top and the bottom, we may follow the following rules:

1.     If the degree of n is higher on top, then the limit is infinity.

2.     If the degree of n is higher on the bottom, then the limit is zero.

3.     If the degree of n is the same in the numerator and denominator, then the limit is the ratio of the leading coeffecients.

Ø  Example:

Example1.

The definition of the derivative of a function at a certain point uses the concept of limits.

Suppose f is a real-valued function, and x₀ is a certain point of its domain in the f. The derivative f’(x₀) f’(x₀) = lim x

Example2.

Find f(x)=

Note: the point x=3 for the function  is meaningless since the denominator cannot be zero, so we should use the limit to predict the value at x=3.

Solution: f(x)==

Ø  Real World Application:

Suppose if I keep tossing a coin as long as it takes, how likely am I to never toss a head?

The possibility of never tossing a head is decreasing. Within the frequency increasing, the limit of the possibility is 0.

The mathematical answer to this is:

P(N)=( )^N

lim_N→∞p(N)=0




Class dismissed!